Kullback Leibler Divergence

Published: 2020-05-24

In this post we will explore the Kullback-Leibler divergence, its properties, and how it relates to Jensen Inequality. Kullback Leibler (KL) divergence is used to measure the probability distribution difference by taking the expected value of the log-ratio between $q(x)$ and $p(x)$ . the formula of KL divergence is given by:

\begin{aligned} KL(q||p) &= \mathbb{E}_{q(x)} \log \frac{q(x)}{p(x)} \\ KL(q||p) &= \int q(x)\log \frac{q(x)}{p(x)}dx \end{aligned}

why we need KL divergence? why don’t we just use distance to measure its difference? using KL divergence we can capture the better difference between the distribution. For example, look at this picture of distribution comparisons:

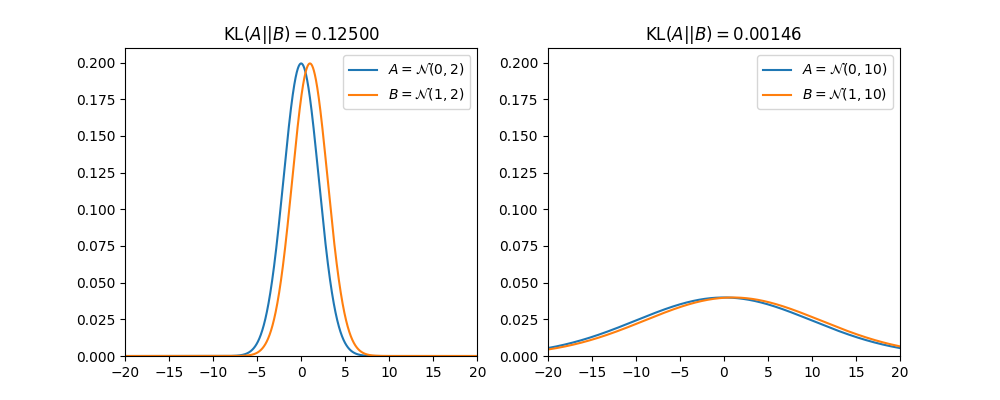
both comparisons have the same parameter distance which is 1. But, graphically we can see that the second comparison is closer than the first one. Using KL divergence, it is shown above that the second comparison “closeness” value is lower than the first one. Now let’s look at the properties of the KL.

Properties of the Kullback Leibler Divergence :

\begin{aligned} \text{1. }KL(q(x)||p(x)) &\neq KL(p(x)||q(x)) &\text{(asymmetric)} \\ \text{2. }KL(q(x)||q(x)) &= 0 \\ \text{3. }KL(q(x)||p(x)) &\geq 0 &\text {(non-negativity)} \end{aligned}

The reason for the 1st property is that when we interchange $q(x)$ and $p(x)$ position (expected value change) it becomes different expression so that KL divergence is not symmetrical. that’s also why KL divergence is not called a distance.

the proof for the 2nd property is as follows:

\begin{aligned} KL(q||q) &= \int q(x)\log \frac{q(x)}{q(x)}dx\\ KL(q||q) &= \int q(x)\log (1) dx\\ KL(q||q) &= \int q(x)\cdot 0 dx\\ KL(q||q) &= 0 \end{aligned}

and lastly the proof of the third property is as follows :

\begin{aligned} - KL(q||p) &= \mathbb{E}_{q(x)} -\log \frac{q(x)}{p(x)} = \mathbb{E}_{q(x)} \log \frac{p(x)}{q(x)} \end{aligned}

Using Jensen Inequality:

\begin{aligned} \mathbb{E}_{q(x)} \log \frac{p(x)}{q(x)} \leq \log\mathbb{E}_{q(x)} \frac{p(x)}{q(x)} \end{aligned}

in the right hand side we have:

\begin{aligned} \log\mathbb{E}_{q(x)} \frac{p(x)}{q(x)} &= \log \int q(x) \frac{p(x)}{q(x)}dx\\ &= \log \int p(x)dx\\ &= \log (1) \\ &= 0 \end{aligned}

back to our inequality we got:

\begin{aligned} \mathbb{E}_{q(x)} \log \frac{p(x)}{q(x)} \leq 0 \end{aligned}

Because -KL is always negative or equal to zero, thus KL is always positive!

references:

update:

(27-06-2023) Scaling y axis of the figures.