Jensen Inequality

Published: 2020-03-07

Jensen Inequality is an inequality in mathematics that relates to the concave/convex function. A function is concave if the line segment between any two points on it lies below the graph of the function. Mathematically we can write:

function $f(x)$ is concave if, if any $a,b,\alpha$ satisfies:

where $0 \leq \alpha \leq 1$, and $a,b \in X$. Here, $X$ is a concave set.

Whereas, in a convex function, the line segment between any two points is lies above the graph. So, we only need to change the $\geq$ sign in equation $(1)$ to $\leq$.

For example $\log(x)$ is a concave function, and $-\log(x)$ is a convex function. The definition above can be visualized as follows:

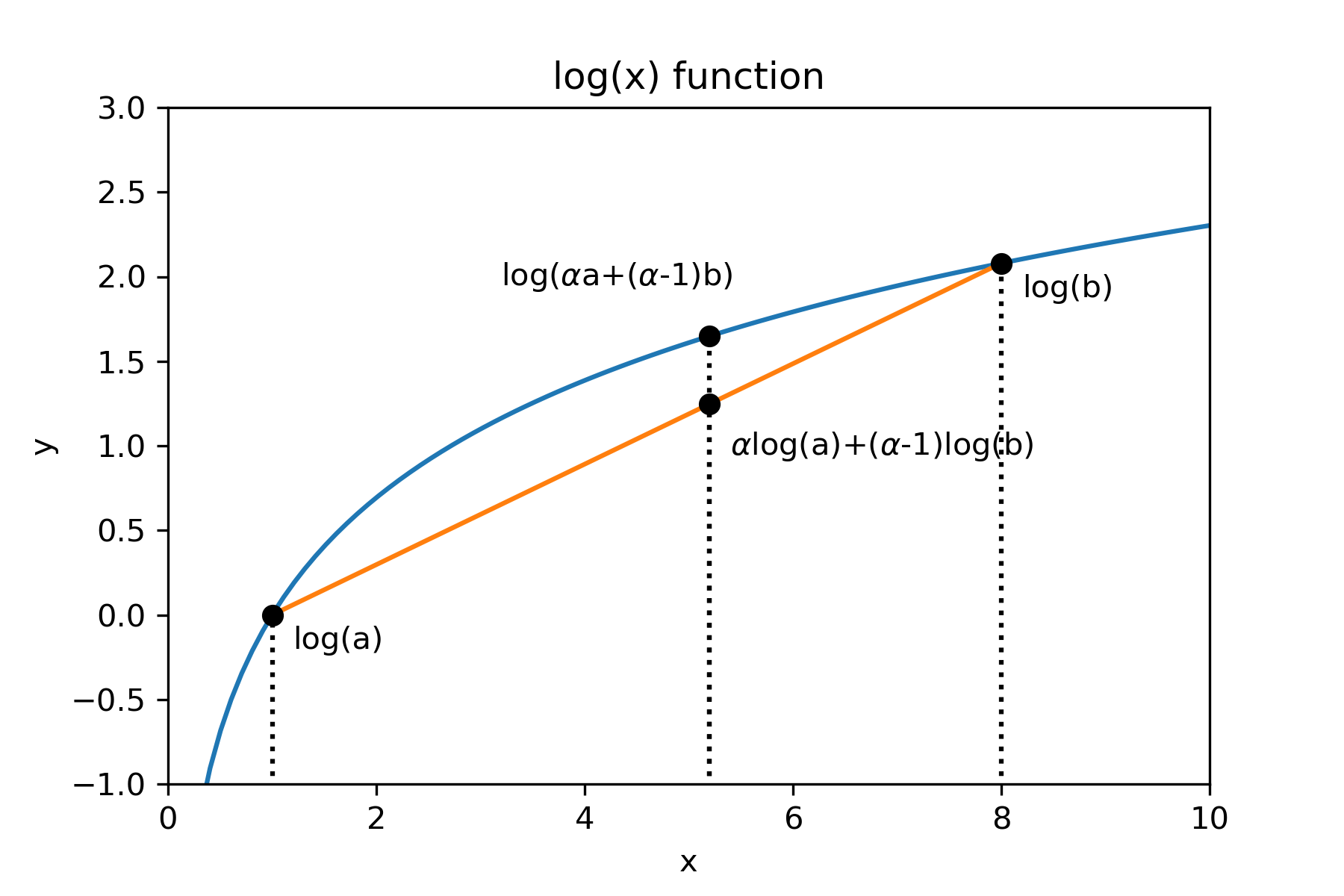
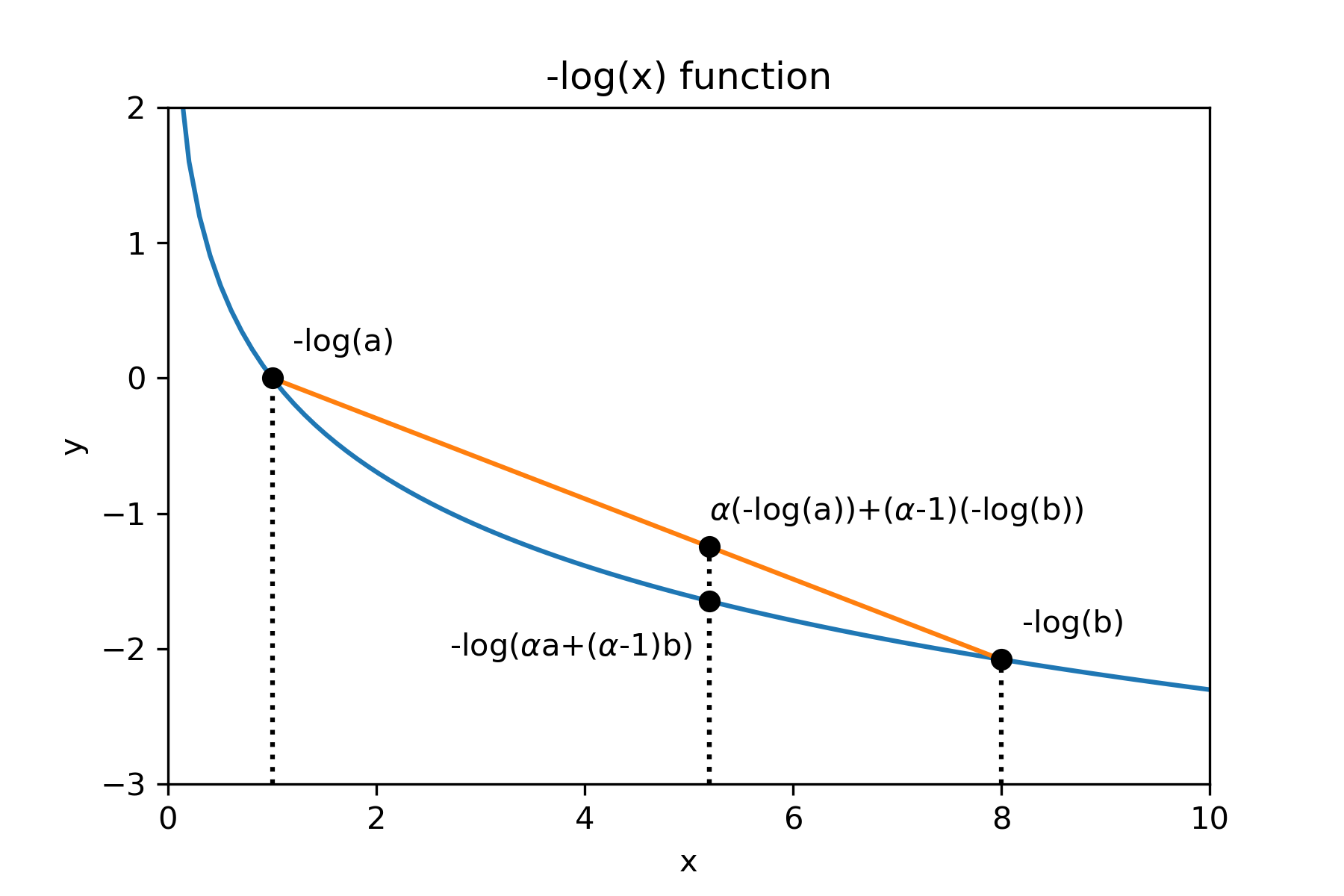
That’s the case for 2 points. Now, consider if we have 3 points instead. If $\alpha_1+\alpha_2+\alpha_3 = 1$ and $\alpha_k \geq 0$ and $f(x)$ is concave:

Thus, using the definition of expectation, we can generalize above equation to (concave and convex respectively):

Thats it, Jensen Inequality is the generalized form of the statement that the secant line of a convex function lies above the graph of the function.

References:

• Wikipedia
• Coursera - HSE bayesian methods in ML